自分は基本的に読書は紙派である。本棚に蔵書として追加されていく達成感があるし、(これはさんざん言われているが)空間記憶や三次元記憶は確かにあると思い込んでいるからだ。しかし徐々にkindleの便利さに気づいてしまい、今や約半数が電子書籍である。メモも付箋も簡単だし、内容によって使い分ければ一層読書が捗りそうだ。お金が許す限りは。
(以下、本編)
かつて文庫本で手に入れて当時売りさばいてしまったものの、内容が面白かったので読み返すために改めてkindleで購入する書籍がいくつかある。この「料理の四面体」も然り。本のタイトルの、本ブログのタイトルのちぐはぐぶりに「はぁ?」となる人もいるだろう。しかし自分にとっての「相手に分かりやすく伝える上での考え方の基本」は未だにこの本にもとづいているのだ。
基本的には垂涎もののグルメ本。しかし終盤はそれらを総括した論理展開。短いながらも、そのバランスが良い本である。それから「四面体」という単語が出てきただけで数学のアレルギー反応を示す必要もない。表紙の三角形が4枚合わさった立体。これだけ想像できれば本書は十分である。

本記事のサマリー:
- わかりやすく説明することは、やっぱりどう考えても必要なこと
- モデル化は非常に汎用性が高い。日常的にも使えるよ
読んだ本
- タイトル:料理の四面体
- 著者:玉村豊男
感想云々
わかりやすく伝えることの必要性
「頭がいい人は難しいことを噛み砕いて簡単に説明できる」。これは自分がかつて信条にもしていた考え方である。しかし徐々に年齢を重ねるたびに、必ずしもそうではないのかもしれない、と思うことになった。なぜなら説明する能力というのはあくまでオプションであって、物事を理解する思考そのものにはあまり関係ないと思うようになったからだ。難しい事柄や多い情報量というのは、できればそのままの状態で吸収できた方がいいように思われる。
では、なぜその上で分かりやすく伝えることが大事なのか。それはシンプルに「時間がかかるから」である。研究で何かを発見したときも、自分がなにか新しいものを設計したときも、営PRするときも、相手を交えた説明・交渉・折衝は免れない。そんなとき、わかりにくい説明は自分だけでなく、相手の時間も当然奪っていることになる。自分も相手も、一つの案件にたくさん時間を費やせるほど暇ではないだろう。しかし伝える方法ひとつで、すべての効率を下げる要因になってしまうのだ。
では、わかりやすく伝えるにはどうすればよいか。そのポイントのひとつとして「モデル化」がある。モデル化は、物事を抽象化して、その構造や関係性を図示する方法である。これは非常に複雑な物事であったり、目に見えないものを「見える化」する方法としてかなり有効な手段だ。次節で具体例を示す。自分は会社に進めるようになってから、とりわけこの手法の重要性を痛感するようになった。
モデル化の具体例(料理を図形で表すと…?)
モデル化の例として、料理を引き合いに出してみる。そもそも、料理は組み合わせ次第で無数に存在する。しかし、そんな料理でさえモデル化して説明できてしまうというのが本書のポイントである。料理の一般原理としては、つぎの4つの要素から成り立っている。
- 火
- 空気
- 水
- 油
この4つの要素を利用して「料理」というモデルは次のように表せるというのが著者の主張だ。
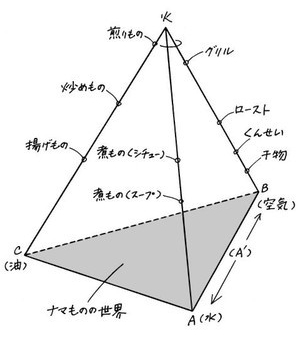
前述の4つの要素を各頂点に置いて、底面は三角形を形成している。そして、ひとつひとつの頂点を結んでいる線が、それぞれの要素に別の要素が絡んでくる料理を表している。つまり「火と空気をつなげる線」=「焼き物」、「火と水をつなげる線」=「煮物」、「火と油をつなげる料理」=「揚げ物」である。それぞれの料理で、各4つの要素がどれだけ介在してくるかで、その料理が四面体のどこに位置するかが変わってくるのだ。モデル化の手法は今までも数あれど、料理を題材にするのは非常に説得力が高いように思える。
汎用性の高い「モデル化」の手法
この「モデル化」は、もちろん料理以外にも適用できる。たとえば「いき」という言葉。江戸時代に生じた「身なりや振る舞いが洗練されていること」を指す言葉であるが、この言葉を文章だけできちんと説明するのは難しそうだ。ところがモデル化を使うと、「いき」の構造は次の図形のOP線上に位置することになる。
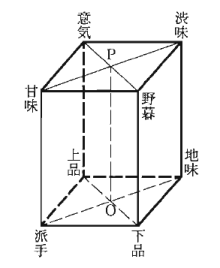
一見ふわっとした「いき」のイメージも「上品」や「野暮」など複数の要素があり、その中で絶妙なバランスで成り立っていることが一目瞭然である。モデル化、恐るべし。
モデル化を使いこなすと、色々と応用が利きそうだ。「仕事」はどうだろう?人によって考え方は様々だろうが、自分の場合は下記のとおりだ(次元が合っているかは置いといて)
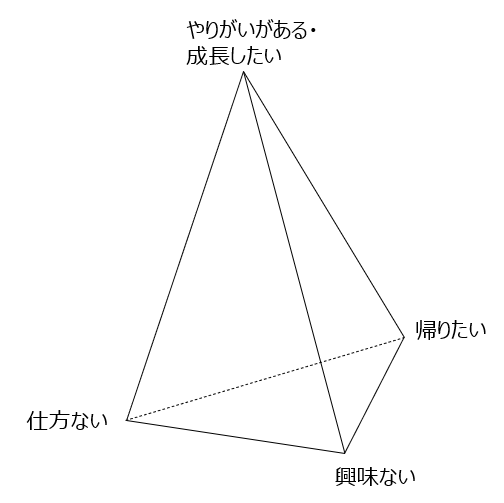
ちなみにこの四面体は少し厄介で、常に重力がはたらいている状態である。モチベーションやらなにやらで頑張って励起し続けないと、油断したら四面体の下面に引きずり降ろされることになるのだ。このように、一見絡み合わないように思える要素も、図解することで新たなアイデアが見えてくる可能性を秘めているのも、モデル化の魅力なのかもしれない。
終わりに
複雑な「料理」がシンプルな図形で表せてしまうのは非常に画期的で、モデル化の有効性は十分に知ることができるだろう。今や必須とも言えるモデル化の考えを学ぶファーストステップとして、本書は大きな助けになるのではないだろうか。本書を読んで料理がうまくなるのかは知らん。
それでは。


